坐標係的控製是通過 QPainter 類。連同 QPaintDevice and QPaintEngine 類, QPainter 形成瞭 Qt 的描繪係統的基礎。 QPainter 用於履行繪製操作, QPaintDevice 是 2 維空間的抽象,在其中描繪可以使用 QPainter ,和 QPaintEngine 提供用於在不同類型設備中繪製的描繪器接口。
The QPaintDevice 類是可以描繪對象的基類:它的繪製能力被繼承由 QWidget , QImage , QPixmap , QPicture ,和 QOpenGLPaintDevice 類。描繪設備的默認坐標係,其擁有位於左上角的原點。 x 值嚮右遞增,和 y 值嚮下遞增。默認單位在基於像素的設備中是 1 像素,而在打印機中是一點 (1/72 英寸)。
映射邏輯 QPainter 坐標到物理 QPaintDevice 坐標的處理是通過 QPainter 的變換矩陣、視口及窗口。默認情況下,邏輯坐標係和物理坐標係重閤。 QPainter 還支持坐標變換 (如:鏇轉和比例縮放)。
圖形圖元的大小 (寬度和高度) 始終對應其數學模型,忽略鋼筆寬度渲染它采用:

|

|
| QRect ( QPoint (1, 2), QPoint (7, 6)) | QLine ( QPoint (2, 7), QPoint (6, 1)) |
| QLine (2, 7, 6, 1) | |
| QRect ( QPoint (1, 2), QSize (6, 4)) | |
| QRect (1, 2, 6, 4) |
當繪製時,像素渲染的控製是通過 QPainter::Antialiasing 渲染提示。
The RenderHint 枚舉用於將標誌指定給 QPainter 可能 (或不可能) 被任何給定引擎遵守。 QPainter::Antialiasing 值指示引擎應對圖元邊緣抗鋸齒若可能的話 (即:通過使用不同顔色光亮度平滑邊緣)。
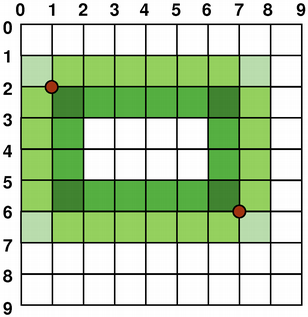
但默認情況下,描繪器 aliased 並應用其它規則:當按 1 像素寬鋼筆渲染時,像素將被渲染到 數學定義點的右側和下方 。例如:

|

|
QPainter painter(this); painter.setPen(Qt::darkGreen); // Using the (x y w h) overload painter.drawRect(1, 2, 6, 4); |
QPainter painter(this); painter.setPen(Qt::darkGreen); painter.drawLine(2, 7, 6, 1); |
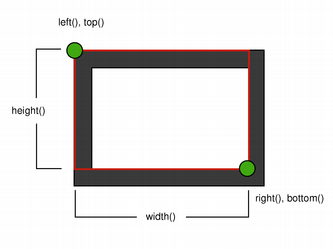
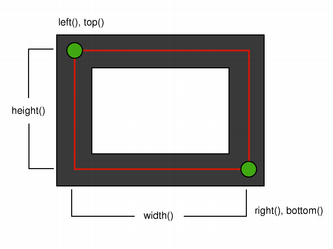
When rendering with a pen with an even number of pixels, the pixels will be rendered symetrically around the mathematical defined points, while rendering with a pen with an odd number of pixels, the spare pixel will be rendered to the right and below the mathematical point as in the one pixel case. See the QRectF 以下簡圖瞭解具體範例。
| QRectF | |
|---|---|

|
|
| 邏輯錶示 | 1 像素寬鋼筆 |
|

|
| 2 像素寬鋼筆 | 3 像素寬鋼筆 |
注意,由於曆史原因,返迴值對於 QRect::right () 和 QRect::bottom () 函數會偏離矩形的真正右下角。
QRect 's right() 函數返迴 left() + width() - 1 and the bottom() 函數返迴 top() + height() - 1. The bottom-right green point in the diagrams shows the return coordinates of these functions.
推薦隻需使用 QRectF 代替: QRectF 類使用浮點坐標定義平麵矩形以提高精度 ( QRect 使用整數坐標),和 QRectF::right () 和 QRectF::bottom () 函數 do 返迴真正右下角。
另外,使用 QRect ,應用 x() + width() and y() + height() to find the bottom-right corner, and avoid the right() and bottom() 函數。
若設置 QPainter 's 抗鋸齒 render hint, the pixels will be rendered symetrically on both sides of the mathematically defined points:
|

|
QPainter painter(this); painter.setRenderHint( QPainter::Antialiasing); painter.setPen(Qt::darkGreen); // Using the (x y w h) overload painter.drawRect(1, 2, 6, 4); |
QPainter painter(this); painter.setRenderHint( QPainter::Antialiasing); painter.setPen(Qt::darkGreen); painter.drawLine(2, 7, 6, 1); |
默認情況下, QPainter 運轉於關聯設備自己的坐標係統中,但它還擁有對仿射坐標變換的完整支持。
You can scale the coordinate system by a given offset using the QPainter::scale () function, you can rotate it clockwise using the QPainter::rotate () function and you can translate it (i.e. adding a given offset to the points) using the QPainter::translate () 函數。

|

|
|

|
| nop | rotate() | scale() | translate() |
You can also twist the coordinate system around the origin using the QPainter::shear () function. All the transformation operations operate on QPainter 's transformation matrix that you can retrieve using the QPainter::worldTransform () function. A matrix transforms a point in the plane to another point.
If you need the same transformations over and over, you can also use QTransform objects and the QPainter::worldTransform () 和 QPainter::setWorldTransform () functions. You can at any time save the QPainter 's transformation matrix by calling the QPainter::save () function which saves the matrix on an internal stack. The QPainter::restore () function pops it back.
One frequent need for the transformation matrix is when reusing the same drawing code on a variety of paint devices. Without transformations, the results are tightly bound to the resolution of the paint device. Printers have high resolution, e.g. 600 dots per inch, whereas screens often have between 72 and 100 dots per inch.
| 指針式時鍾範例 | |
|---|---|

|
The Analog Clock example shows how to draw the contents of a custom widget using
QPainter
's transformation matrix.
We recommend compiling and running this example before you read any further. In particular, try resizing the window to different sizes. |
void AnalogClockWindow::render(QPainter *p) { static const QPoint hourHand[3] = { QPoint(7, 8), QPoint(-7, 8), QPoint(0, -40) }; static const QPoint minuteHand[3] = { QPoint(7, 8), QPoint(-7, 8), QPoint(0, -70) }; QColor hourColor(127, 0, 127); QColor minuteColor(0, 127, 127, 191); p->setRenderHint(QPainter::Antialiasing); p->translate(width() / 2, height() / 2); int side = qMin(width(), height()); p->scale(side / 200.0, side / 200.0);
We translate the coordinate system so that point (0, 0) is in the widget's center, instead of being at the top-left corner. We also scale the system by
This will give us a 200 x 200 square area, with the origin (0, 0) in the center, that we can draw on. What we draw will show up in the largest possible square that will fit in the widget. 另請參閱 窗口/視口轉換 章節。
QTime time = QTime::currentTime();
p->save();
p->rotate(30.0 * ((time.hour() + time.minute() / 60.0)));
p->drawConvexPolygon(hourHand, 3);
p->restore();
We draw the clock's hour hand by rotating the coordinate system and calling QPainter::drawConvexPolygon (). Thank's to the rotation, it's drawn pointed in the right direction.
The polygon is specified as an array of alternating
x
,
y
values, stored in the
調用 QPainter::save () 和 QPainter::restore () surrounding the code guarantees that the code that follows won't be disturbed by the transformations we've used.
p->save();
p->rotate(6.0 * (time.minute() + time.second() / 60.0));
p->drawConvexPolygon(minuteHand, 3);
p->restore();
We do the same for the clock's minute hand, which is defined by the four points (1, 0), (0, 1), (-1, 0), and (0, -40). These coordinates specify a hand that is thinner and longer than the minute hand.
p->setPen(minuteColor);
for (int j = 0; j < 60; ++j) {
if ((j % 5) != 0)
p->drawLine(92, 0, 96, 0);
p->rotate(6.0);
}
Finally, we draw the clock face, which consists of twelve short lines at 30-degree intervals. At the end of that, the painter is rotated in a way which isn't very useful, but we're done with painting so that doesn't matter. |
|
For more information about the transformation matrix, see the QTransform 文檔編製。
當描繪采用 QPainter ,使用邏輯坐標指定點,然後轉換成描繪設備的物理坐標。
邏輯坐標到物理坐標的映射的處理是通過 QPainter 的世界變換 worldTransform() (described in the 變換 章節),和 QPainter 's viewport() and window() . The viewport represents the physical coordinates specifying an arbitrary rectangle. The "window" describes the same rectangle in logical coordinates. By default the logical and physical coordinate systems coincide, and are equivalent to the paint device's rectangle.
Using window-viewport conversion you can make the logical coordinate system fit your preferences. The mechanism can also be used to make the drawing code independent of the paint device. You can, for example, make the logical coordinates extend from (-50, -50) to (50, 50) with (0, 0) in the center by calling the QPainter::setWindow () 函數:
QPainter painter(this); painter.setWindow(QRect(-50, -50, 100, 100));
Now, the logical coordinates (-50,-50) correspond to the paint device's physical coordinates (0, 0). Independent of the paint device, your painting code will always operate on the specified logical coordinates.
By setting the "window" or viewport rectangle, you perform a linear transformation of the coordinates. Note that each corner of the "window" maps to the corresponding corner of the viewport, and vice versa. For that reason it normally is a good idea to let the viewport and "window" maintain the same aspect ratio to prevent deformation:
int side = qMin(width(), height()) int x = (width() - side / 2); int y = (height() - side / 2); painter.setViewport(x, y, side, side);
If we make the logical coordinate system a square, we should also make the viewport a square using the QPainter::setViewport () function. In the example above we make it equivalent to the largest square that fit into the paint device's rectangle. By taking the paint device's size into consideration when setting the window or viewport, it is possible to keep the drawing code independent of the paint device.
Note that the window-viewport conversion is only a linear transformation, i.e. it does not perform clipping. This means that if you paint outside the currently set "window", your painting is still transformed to the viewport using the same linear algebraic approach.

The viewport, "window" and transformation matrix determine how logical QPainter coordinates map to the paint device's physical coordinates. By default the world transformation matrix is the identity matrix, and the "window" and viewport settings are equivalent to the paint device's settings, i.e. the world, "window" and device coordinate systems are equivalent, but as we have seen, the systems can be manipulated using transformation operations and window-viewport conversion. The illustration above describes the process.
另請參閱 指針式時鍾窗口範例 .